混淆矩阵
| 正类 | 负类 | |
|---|---|---|
| 预测为正 | TP（真正） | FP（假正） |
| 预测为负 | FN（假负） | TN（真负） |
- TP（真正）: 将正类预测为正类数
- FP（假正）: 将负类预测为正类数（误报，Type I error）
- TN（真负）: 将负类预测为负类数
- FN（假负）: 将正类预测为负类数（漏报，Type II error）
几种指标
准确率（accuracy）
准确率就是所有预测正确的样本占总样本数的比例。 \[Accuracy = \frac{TP + TN}{TP + FP + TN + FN}\]
正确率 / 精确率（Precision） / 查准率
真正样本数占所有正类样本数的比例
\[P = Precision= \frac{TP}{TP + FP}\]
TPR（True Positive Rate） / 灵敏度（Sensitivity） / 召回率（Recall） / 查全率
真正样本数占所有预测为正类样本数的比例
\[R = Recall = TPR= \frac{TP}{TP + FN}\]
TNR（True Negative Rate） / 特异度（Specificity）
真负样本数占所有预测为负类样本数的比例
\[TNR= \frac{TN}{TN + FP}\]
FNR（False Negative Rate） / 漏报率
假负样本数占所有预测为负类样本数的比例
\[FNR= \frac{FN}{TN + FP} = 1 - TNR\]
FPR（False Positive Rate） / 误报率
假正样本数占所有预测为负类样本数的比例
\[FPR= \frac{FP}{FP+ TN} = 1 - TPR\]
PR曲线（Precision-Recall Curve）
理解召回率(Recall)和精确率(Precision)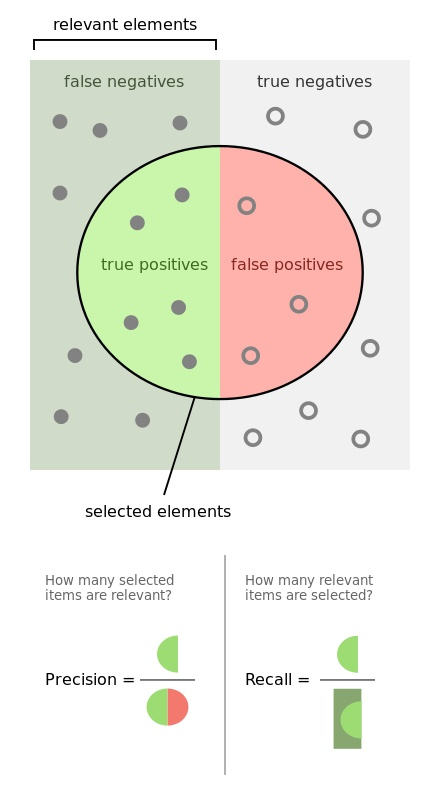 
PR曲线
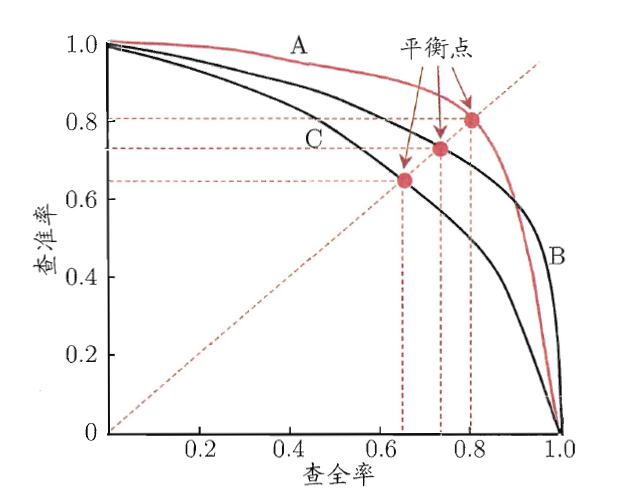PR空间将查全率/召回率(Recall)定义为X轴，查准率/精确率(Precision)定义为Y轴。
可根据分类器的预测结果对样例进行排序，排在前面的是分类器认为最可能是正例的样本，排在最后的则是分类器认为最不可能是正例的样本。按此顺序逐个把样本作为正例进行预测，则每次可以计算出当前的查全率、查准率，并构造PR曲线。
由于PR曲线的曲线下面积不方便估算，因此需要用别的值来作为综合考虑Recall和Precision的性能度量。BEP（Break-Even Point，平衡点）为PR曲线上Recall=Precision时的取值，可以用于找出在Recall和Precision取得双高的分类器。
但BEP还是过于简化，因此引出了F1值。
F1值（F1-score）
精确率(Precision)和召回率(Recall)的调和均值 \[F1 = \frac{2 * P * R}{P + R} = \frac{2 * TP}{样本总数 + TP - TN} = \frac{2 * TP}{2 * TP + FN + FP}\]
一些场景中对精确率(Precision)和召回率(Recall)的重视程度不同，因此定义F1的一般形式 \[F_\beta = \frac{(1 + \beta^2) * P * R}{(\beta^2 * P) + R}\]
ROC-AUC（Area under the Curve of ROC）
ROC曲线
ROC曲线，即接收者操作特征曲线（receiver operating characteristic curve）。
ROC空间将FPR（False Positice Rate）定义为X轴，TPR（True Positive Rate）定义为 Y 轴。
给定一个二元分类模型和它的阈值，就能从所有样本的（阳性／阴性）真实值和预测值计算出一个 (X=FPR, Y=TPR) 座标点。 从 (0, 0) 到 (1,1) 的对角线将ROC空间划分为左上／右下两个区域，在这条线的以上的点代表了一个好的分类结果（胜过随机分类），而在这条线以下的点代表了差的分类结果（劣于随机分类）。
完美的预测是一个在左上角的点，在ROC空间座标 (0,1)点，X=0 代表着没有伪阳性，Y=1 代表着没有伪阴性（所有的阳性都是真阳性）；也就是说，不管分类器输出结果是阳性或阴性，都是100%正确。一个随机的预测会得到位于从 (0, 0) 到 (1, 1) 对角线（也叫无识别率线）上的一个点；最直观的随机预测的例子就是抛硬币。
ROC-AUC
ROC-AUC为ROC曲线下方的面积。
AUC的3种取值对应的ROC曲线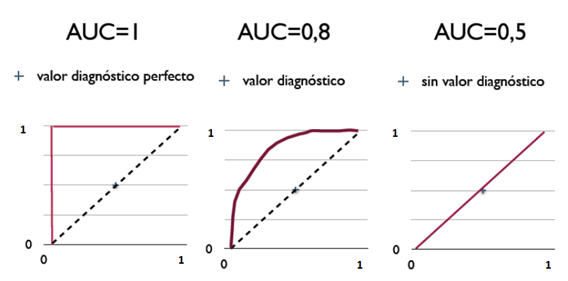 
ROC-AUC的意义是：
- 因为是在1x1的方格里求面积，AUC必在0~1之间
- 一般来说，如果ROC是光滑的，那么基本可以判断没有太大的overfitting
- 假设阈值以上是阳性，以下是阴性；若随机抽取一个阳性样本和一个阴性样本，分类器正确判断阳性样本的值高于阴性样本之机率=AUC
- AUC值越大的分类器，正确率越高
从AUC判断分类器优劣的标准：
- AUC = 1，是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。绝大多数预测的场合，不存在完美分类器
- 0.5 < AUC < 1，优于随机猜测。这个分类器妥善设定阈值的话，能有预测价值
- AUC = 0.5，跟随机猜测一样，模型没有预测价值
- AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测
适用场景
准确率（accuracy）是很常用的一种标准，但是在有类不平衡（class imbalance）问题的时候不好使。
举个例子，当100个样本里99个是正样本，1个是负样本的时候，如果分类器直接把所有的样本预测为正样本，这个分类器就有99%的准确率了，但实际上这个分类器一个负样本都分辨不出来。
精确率（Precision）可以在要求不错选的时候使用。
要求尽量不将负类样本预测为正类的，即不错选任何正类样本。使用场景为嫌疑人定罪，垃圾邮件分类等。这种情况下可以在Recall符合一定条件的情况下选择Precision最高的分类器。
召回率（Recall）可以在要求不错放的时候使用。
要求尽量所有正类样本都被挖掘出来，不错放过任何正类样本。使用场景为地震预测，癌症预测等。这种情况下可以在Precision符合一定条件的情况下选择Recall最高的分类器。
PR曲线在正类样本很稀少的情况下，比起ROC曲线能更有效地反应分类器的好坏。
因为PR曲线对于类不平衡问题相当敏感，能在正类样本稀少的情况根据precision有明显变化。
举一个列子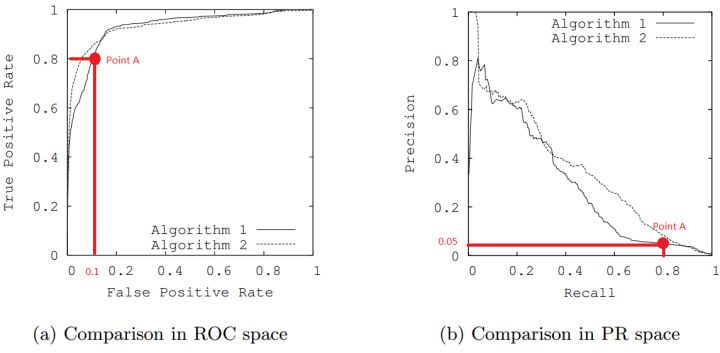 
上图中为ROC及PR曲线的对比，根据ROC曲线，感觉两个算法效果都还不错（足够接近左上角），而PR曲线则显示效果不好（不够接近右上角）。
分析Algorithm 1上的Point A，这点上 recall = TPR = 0.8
假设有100个正类样本，则有 TP = 80
根据图（b）中 precision = 0.05，可以得出 FP = 1520
根据图（a）中 FPR= 0.1，可以得出 TN = 13680
则样本总体情况应该是正类样本100个，负类样本15200个，TP = 80，FP = 1520，TN = 13680，FN = 20
也就是说分类器将1600个样本分为正类，而其中只有80个真正样本。这样一个分类器效果确实不算好。
另外再例举一个欺诈检测的问题
200w样本中有100个正类样本。
- Algorithm 1：预测出100个正类样本，其中有90个真正样本
- Algorithm 2：预测出1000个正类样本，其中有90个真正样本
可以直观的看出来Algorithm 1更好，因为错选的更少。
在ROC曲线中：
- Algorithm 1：TPR=90/100=0.9, FPR= 10/1,999,900=0.00000500025
- Algorithm 2：TPR=90/100=0.9, FPR=910/1,999,900=0.00045502275
FPR差为0.0004500225，即在X=0.9时，两条曲线Y轴上相差0.0004500225
在PR曲线中：
- Algorithm 1：precision=0.9, recall=0.9
- Algorithm 2：precision=0.09, recall= 0.9
Precision差为0.81，即在X=0.9时，两条曲线Y轴上相差0.81
因此在PR中两种算法的优劣差异能更明显的显示出来。
ROC-AUC是一个最稳定的选择，适合在正负样本数量都足够的时候选择。
当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。ROC曲线对非平衡数据不敏感。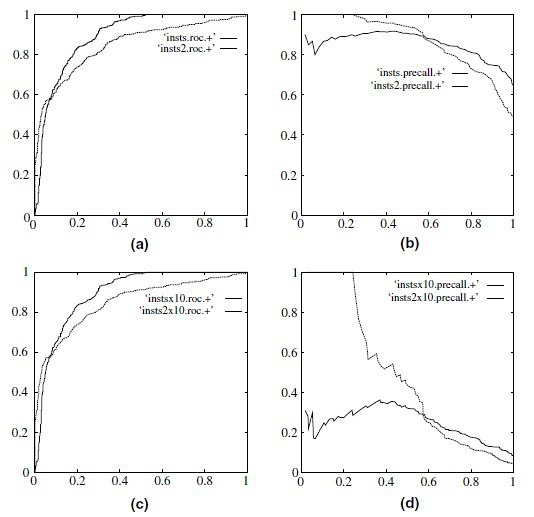 
(a)和(c)为ROC曲线，(b)和(d)为PR曲线。(a)和(b)为正负样本1:1时的ROC曲线和PR曲线，二者比较接近。(c)和(d)是将负样本的数量增加到原来的10倍后的ROC曲线和PR曲线。可以明显的看出，ROC曲线基本保持原貌，而PR曲线则变化较大。