使用 keras 复现 MemN2N

keras 复现 memory networks 系列

概述

参考论文：《End-To-End Memory Networks》

数据集：bAbI-tasks

最终源码：keras-MemN2N（GitHub）

前期工作：

论文相关

数据相关

数据集里每个任务有 \(I\)（\(I\le 320\)）个句子作为 input \(\{x_i\}\)
词典大小 \(V=177\)

维度计算

架构图 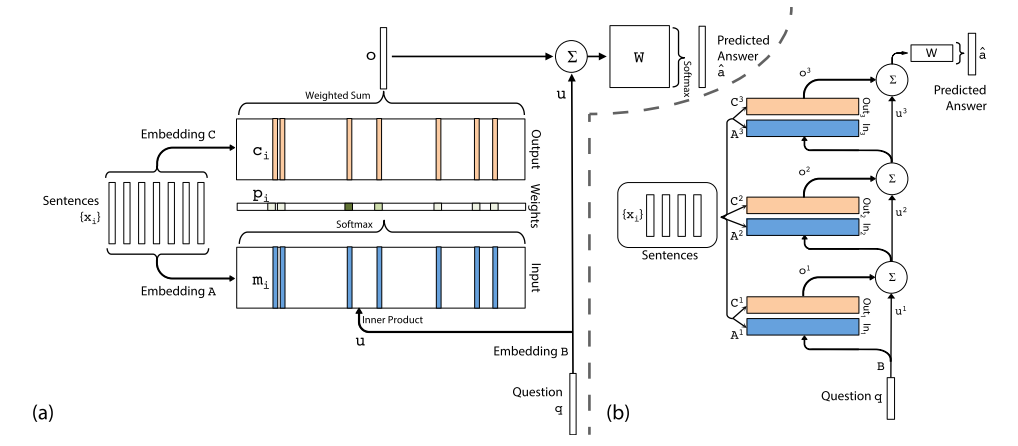Alt text

梳理一下维度关系

以 bAbI-task-qa1 为例进行计算

vocab_size = 20
- 字典大小为 20
story.shape = (None, 10, 6)
- 一个 story 最多 10 个句子
- 每个句子最多 6 个单词
query.shape = (None, 6)
- query 的单词数和 story 里的单词数要统一，这里就定为 6（实际上 query 都是 3 个词）
m_emb.shape = (None, 10, d)
- story 通过了一个 (embedding_size, vocab_size) 的 embedding 矩阵 \(A\) 得到的输出，d 为 embedding_size
- 架构图里的 Input（\(m_i\) 的 shape 为 (None, d)）
- 相当于每个句子 embedding 成了一个 d 维向量
- 参考公式：\(m_i=\sum_jAx_{ij}\)，其中 \(x_{ij}\) 为第 \(i\) 个句子的第 \(j\) 个词（BoW表示句子，最简单的一个公式）
c_emb.shape = (None, 10, d)
- 基本同 m_emb，embedding 矩阵为 \(C\)，\(c_i=\sum_jCx_{ij}\)
- 架构图里的 Output（\(c_i\) 的 shape 为 (None, d)）
u_emb.shape = (None, d)
- query 通过了一个 (embedding_size, vocab_size) 的 embedding 矩阵 \(B\) 得到的输出
- 架构图里的 \(u\)
- 参考公式：\(u = \sum_jBq_j\)
probs.shape = (None, 10)
- 参考公式：\(p_i=Softmax(u^Tm_i)\)
o_weight.shape = (None, d)
- 参考公式：\(o=\sum\limits_ip_ic_i\)
answer.shape = (None, 20)
- 参考公式：\(\hat a = Softmax(W(o+u))\)
- 最后的输出应该是字典里的一个词，所以维度是词典的大小

细节设计

默认使用 \(K=3\) hops 模型，使用 Adjacent 权重取值方式。

几种设计选择：

Sentence Representation：
- BoW
- Position Encoding（PE）
  - \(m_i = \sum_jl_j\cdot Ax_{ij}\)（\(\cdot\) 是 element-wise multiplication）
  - \(l_{kj}=(1-j/J)-(k/d)(1-2j/J)\)（\(J\) 是句子里单词的数量）
Training on all 20 tasks：
- Independently
- Jointly
Phase Training：
- Linear start（LS）
- Softmax
Hops： 1~3

论文最终数据

错误率表 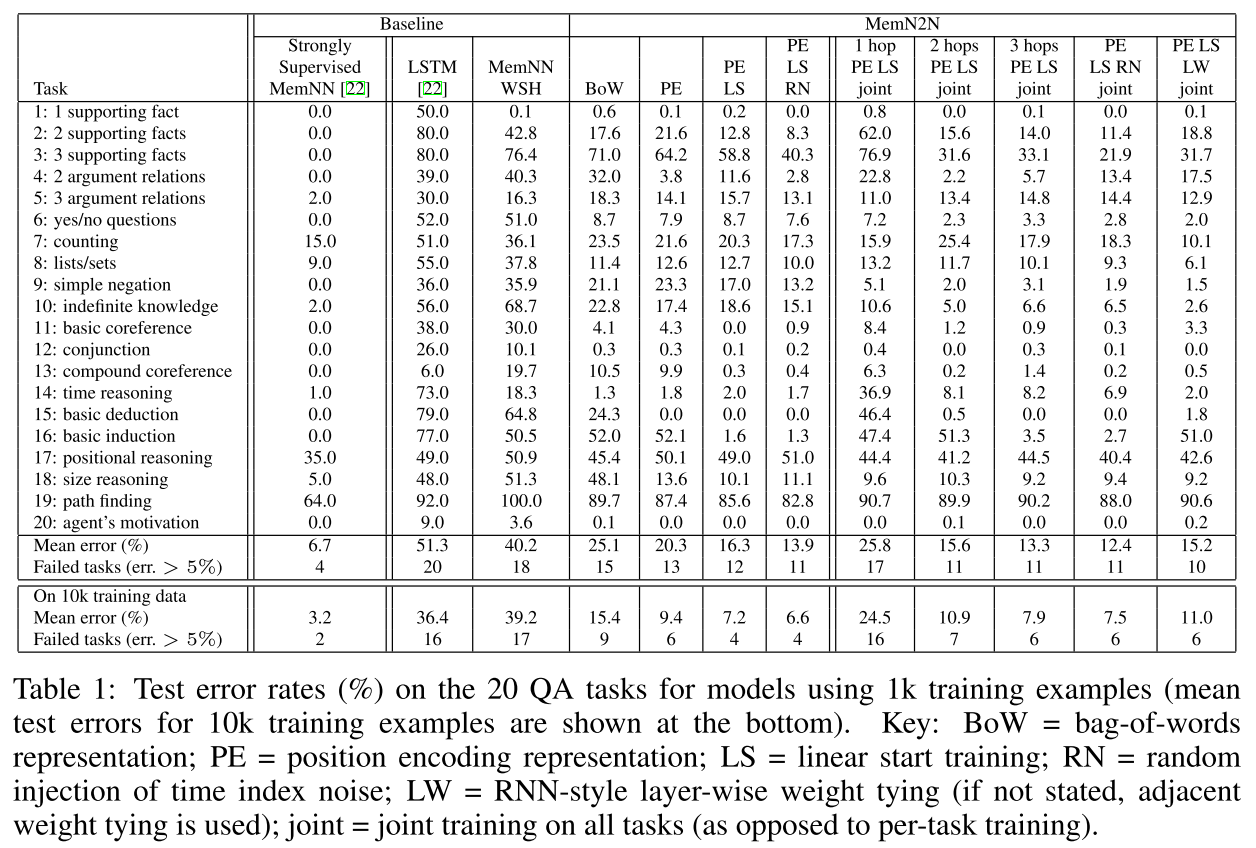Alt text

实现

Keras 的 example 里有一个 babi_memnn.py，说是照着论文复现的，可惜连数据预处理都没对上（代码里直接把一个 tasks 所有句子拼接成一句了），而且也没有实现多 hop，也没有实现论文里 PE、LS 之类的改进，甚至还把模型里最后一层强行改成了 LSTM。完全不能算复现，参考价值也不大。数据预处理部分参考一个 MemN2N 的 tensorflow 实现。

基本实现

从以最简单的 BoW + Adjacent 为例子

用现有层搭建网络

输入部分

1 2	story = Input(shape=(max_story_size, sentence_size,)) question = Input(shape=(sentence_size,))

初始化嵌入层，因为使用 Adjacent 类的权重（\(A^{k+1}=C^k,W^T=C^K,B=A^1\)），所以 \(k\) hops 的模型只需要训练 \(k+1\) 个嵌入矩阵

Embedding_layer = []
for i in range(k_hop + 1) :
    Embedding_layer.append(Embedding(input_dim=vocab_size, output_dim=d, 
                            embeddings_initializer='random_normal'))

计算第一层的 \(m\) 、\(c\) 和 \(u\)，注意 \(m\) 和 \(u\) 使用的是嵌入矩阵 \(A^1\)，\(c\) 使用的是 \(A^2=C^1\)。
以 \(m\) 为例，因为经过嵌入层之后的 shape=(None, 10, 6, d)，而我们需要第二维上的 6 个数字之和并把这一维直接消掉才算能得到目标 shape=(None, 10, d)，所以这里用了一个Lambda层来进行求和操作，\(u\)、\(c\) 同理，就是要注意 \(u\) 是在第一维上求和。

m_emb = Embedding_layer[0](story)
m_emb = Lambda(lambda x: K.sum(x, axis=2))(m_emb)
u_emb = Embedding_layer[0](question)
u_emb = Lambda(lambda x: K.sum(x, axis=1))(u_emb)
c_emb = Embedding_layer[1](story)
c_emb = Lambda(lambda x: K.sum(x, axis=2))(c_emb)

接下来计算权重 \(p_i=Softmax(u^Tm_i)\)，为了进行 \(u^Tm_i\)这一步，我先把\(u^T\)复制到和\(m_i\)维度一样，然后进行 element-wise multiplication，然后再和上面一样进行求和降维（总觉得应该还有更优雅点的实现……

u_temp = Lambda(lambda x: K.expand_dims(x, 1))(u_emb)
u_temp = Lambda(lambda x: K.tile(x, (1, max_story_size, 1)))(u_temp)
probs = multiply([m_emb, u_temp])
probs = Lambda(lambda x: K.sum(x, axis=2))(probs)
probs = Activation('softmax')(probs)

然后计算加权和 \(o=\sum\limits_i p_ic_i\)，也是上面那种复制填充维度，element-wise multiplication，再求和降维

probs_temp = Lambda(lambda x: K.expand_dims(x, 2))(probs)
probs_temp = Lambda(lambda x: K.tile(x, (1, 1, d)))(probs_temp)
o_weight = multiply([c_emb, probs_temp])
o_weight = Lambda(lambda x: K.sum(x, axis=1))(o_weight)

最后求输出 \(\hat a = Softmax(W(o+u))\)

1 2	answer = Dense(vocab_size, kernel_initializer='random_normal')(u_emb[-1]) answer = Activation('softmax')(answer)

这里有一个问题，就是在 Adjacent 权重取值下，最后的 \(W\) 无法取到 \(W^T=C^K\)，于是最后还是决定直接封装一个层出来。

自己封装一个 MemN2N 层

class MemN2N(Layer):

    def __init__(self, max_story_size, sentence_size, vocab_size, embedding_size, k_hop, **kwargs):
        self.max_story_size = max_story_size
        self.sentence_size = sentence_size
        self.vocab_size = vocab_size
        self.embedding_size = embedding_size
        self.k_hop = k_hop
        super(MemN2N, self).__init__(**kwargs)

    def build(self, input_shape):
        self.emb_A = [0] * (self.k_hop + 1)
        for i in range(self.k_hop + 1):
            self.emb_A[i] = self.add_weight(name='Embedding_' + str(i),
                                shape=(self.vocab_size, self.embedding_size),
                                initializer='uniform',
                                trainable = True)

        super(MemN2N, self).build(input_shape)
        
    def call(self, inputs):
        story = inputs[0]
        question = inputs[1]
        
        if K.dtype(story) != 'int32':
            story = K.cast(story, 'int32')
        if K.dtype(question) != 'int32':
            question = K.cast(question, 'int32')
            
        u_emb = K.sum(K.gather(self.emb_A[0], question), axis=1)
        for i in range(self.k_hop) :
            m_emb = K.sum(K.gather(self.emb_A[i], story), axis=2)
            c_emb = K.sum(K.gather(self.emb_A[i + 1], story), axis=2)
            
            u_temp = K.tile(K.expand_dims(u_emb, 1), (1, self.max_story_size, 1))
            probs = K.softmax(K.sum(m_emb * u_temp, axis=2))
            probs = K.tile(K.expand_dims(probs, 2), (1, 1, self.embedding_size))
            u_emb = K.sum(c_emb * probs, axis=1) + u_emb
 
        output = K.dot(u_emb,  K.transpose(self.emb_A[-1]))
        output = K.softmax(output)
        return output

    def compute_output_shape(self, input_shape):
        return (input_shape[0], self.vocab_size)

思路和用现有层差不多，只是能够取到 \(W^T=C^K\) 了。

效果很差，无论是现有层还是自定义的层，task-1 只能到 0.66+，但是 task-20 能到 1（数据集 1k 还是 10k 都差不多，hop 取 3 和取 1 也差不多）

待续