《End-To-End Memory Networks》

Posted on | In |

arxiv
Facebook AI
2015.03

本文主要是为了解决之前提出的《Memory Networks》存在的问题：Memory Networks 训练中难以进行反向传播的计算，且网络的每一层均需要 supervision。

其实这缺陷就是因为 Memory Networks 不是端到端的，因此本文提出 End-to-End Memory Networks（MemN2N）来解决这个问题。

本文框架来源于 Memory Networks ，又可以看作是具有多步计算的 RNNsearch

实现：MemN2N-tensorflow

主要工作

  • 提出 end-to-end memory networks 架构

模型

架构图 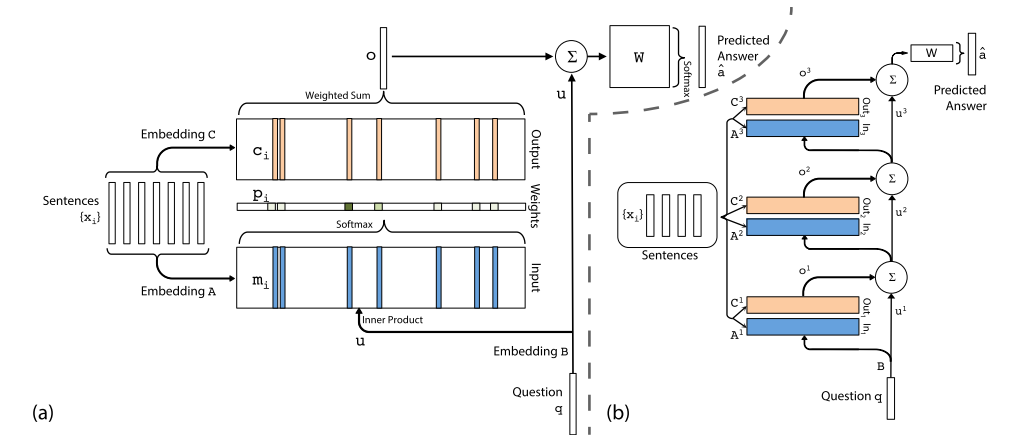Alt text (a) 为单层模型，(b) 为多层模型

给定输入 \(x_1,...,x_n\)，查询（query）\(q\)，模型输出回答 \(a\)

单层模型

参考上图 (a)

  • Input memory representation
    • 给定输入 \(\{x_i\}\)，首先将其 embed 为 \(d\) 维的 memory 向量 \(\{m_i\}\)，由 embedding 矩阵 \(A\) 获得
    • 给定的查询 \(q\) 也 embed 为 \(d\) 维获得内部状态（internal state）\(u\)，由 embedding 矩阵 \(B\) 获得
    • 在 embedding 空间里计算 \(u\) 和 \(m_i\) 的相似度（使用softmax计算内积）：\(p_i=Softmax(u^Tm_i)\)
  • Output memory representation
    • 每个 \(x_i\) 有一个相关输出向量 \(c_i\)，由 embedding 矩阵 \(C\) 获得
    • response 向量 \(o = \sum\limits_ip_ic_i\)
  • Generating the final prediction
    • 预测标签 \(\hat a=Softmax(W(o+u))\)，\(W\) 为训练参数

多层模型

参考上图 (b)

  • 每一层的输入 \(u^{k+1}=u^k+o^k\)
  • 每一层的 \(m_i\)，\(c_i\) 都由 embedding 矩阵 \(A^k\)，\(C^k\) 获得
  • 网络最终输出 \(\hat a=Softmax(Wu^{K+1})=Softmax(W(o^K+u^K))\)

两种权重取值方法：

  1. Adjacent
    • 每一层的输出 embedding 矩阵是下一层的输入 embedding 矩阵（\(A^{k+1}=C^k\)）
    • 预测矩阵和输出 embedding 矩阵相同（\(W^T=C^K\)）
    • question 的 embedding 矩阵和第一层的输入 embedding 矩阵相同（\(B=A^1\)）
  2. Layer-wise（RNN-like）
    • 输入输出 embedding 矩阵每层均相同（\(A^1=A^2=...=A^K, C^1=C^2=...=C^K\)）
    • 应用线性映射 \(H\) 获得 \(u^{k+1}\)：\(u^{k+1} = Hu^k+o^k\)
    • 这种取值方法和传统 RNN 很像（把 \(u\) 看成是 hidden state），只是明确规定了在 \(K\) 跳过程中保存 outputs 到 memory 里（soft），而不是像 RNN 那样对它们进行采样（sampling），因此就在输出结果前多了几步计算（这段和RNN的不同点没理解到位）

Here, unlike a standard RNN, we explicitly condition on the outputs stored in memory during the K hops, and we keep these outputs soft, rather than sampling them. Thus our model makes several computational steps before producing an output meant to be seen by the “outside world”.

读后感

感觉这个应该是加入了 Attention 的思想，就是那个加权平均用到的 \(p_i\)
有了这个端到端的架构之后，MemNNs 才有了实用价值